分享:高碳鋼連鑄坯大區(qū)域C元素分布不均勻度
1.
2.
基于典型高碳鋼鑄坯低倍組織灰度圖,引入標(biāo)準(zhǔn)差、差分盒維數(shù)和慣性矩,探討一種大區(qū)域主要偏析元素(C)分布不均勻度定量表征的簡易方法。結(jié)果表明:標(biāo)準(zhǔn)差、差分盒維數(shù)和慣性矩可以有效地綜合表征C元素分布不均勻度;且等軸晶區(qū)C元素分布不均勻度高于柱狀晶區(qū),平均相差20.85%。對比發(fā)現(xiàn),標(biāo)準(zhǔn)差主要基于灰度值統(tǒng)計特性,差分盒維數(shù)和慣性矩結(jié)合了灰度值統(tǒng)計信息和空間分布信息;并且差分盒維數(shù)具有尺度獨立性,受灰度圖尺寸和分辨率的影響較小,而慣性矩對微區(qū)C元素分布不均勻度變化會更加敏感。此外,標(biāo)準(zhǔn)差主要受到大型偏析點(> 1 mm2)影響,而差分盒維數(shù)和慣性矩主要受中型偏析點(0.1~1 mm2)影響。本工作可為高碳鋼鑄坯大區(qū)域C元素分布不均勻度的全面衡量及精細(xì)化質(zhì)量評判提供新的參考方法。
關(guān)鍵詞:
高碳鋼具有高的強(qiáng)度和硬度,高的彈性極限和疲勞極限,被廣泛應(yīng)用于船舶、化工、機(jī)械等領(lǐng)域[1,2]。由于其C含量高、溶質(zhì)分配系數(shù)低[3],導(dǎo)致高碳鋼的連鑄過程凝固區(qū)間大,易產(chǎn)生偏析和縮孔等內(nèi)部質(zhì)量缺陷,因此C元素是高碳鋼中的主要偏析元素。偏析是合金凝固過程中溶質(zhì)元素在固相和液相中再分配的結(jié)果,表現(xiàn)為從鑄坯表面到中心或沿鑄坯軸向大區(qū)域范圍(如厘米范圍以上)元素分布的不均勻性[4]。偏析元素分布不均勻現(xiàn)象易使連鑄坯產(chǎn)生裂紋或失效[5~7]等質(zhì)量問題,從而降低最終產(chǎn)品的力學(xué)性能。因此,為了更精細(xì)地評價與優(yōu)化高碳鋼產(chǎn)品質(zhì)量,需要對其大區(qū)域C元素分布不均勻度展開專門研究。
以往,研究者[8,9]對C元素分布不均勻度的研究主要從形貌和成分含量2個方面進(jìn)行。前者一般是通過熱酸洗獲取鑄坯的偏析形貌,然后根據(jù)偏析區(qū)域的尺寸、數(shù)目的分布特征以及與宏觀評級圖的對比來定性判斷偏析元素分布不均勻度;對于后者,主要基于鉆孔取樣化學(xué)分析法[10]、電子探針[11]和金屬原位分析儀[12]等方法獲取元素含量,然后通過偏析指數(shù)[13]、均方差[14]等對鑄坯的元素分布不均勻度進(jìn)行定量評判。但是,以上的定性方法易造成較大偏差;而定量方法中鉆孔取樣化學(xué)分析法往往是通過局部某幾點元素含量反映整體元素分布不均勻度,且電子探針等電子顯微方法測量區(qū)域太小,而金屬原位分析儀試樣準(zhǔn)備相對繁瑣,對C含量測量準(zhǔn)確度有限,難以應(yīng)用于實際鋼廠大試樣的評判。因此,針對不同組織區(qū)域內(nèi)元素分布不均勻度的判斷可能會存在不同的結(jié)果。例如,有學(xué)者[15]認(rèn)為等軸晶區(qū)內(nèi)部質(zhì)量更好,成分分布更均勻,希望增加等軸晶比例。然而,另一些研究[16]指出柱狀晶的偏析比等軸晶要少,結(jié)構(gòu)更為致密,希望得到定向凝固組織。可見,柱狀晶區(qū)與等軸晶區(qū)元素分布不均勻度高低的問題尚存在爭議,這使得人們無法精確評價鑄坯不同組織的質(zhì)量。目前定量表征高碳鋼鑄坯大區(qū)域C元素分布不均勻度仍是一個難題,其一是難以獲取大區(qū)域C元素含量分布;其二是沒有具體方法衡量大區(qū)域C元素分布不均勻度。另外,二維大區(qū)域元素分布不均勻度不是一個單一的概念,其包括整體平均不均勻度、局部分布不均勻度等方面;同時元素分布不均勻度會因數(shù)據(jù)尺度與分析范圍的不同而改變。因此,有必要尋找一套有效且能綜合表征鑄坯大區(qū)域范圍內(nèi)偏析元素分布不均勻度的實用方法。本工作提出的大區(qū)域偏析元素分布不均勻度和宏觀偏析雖均指宏觀區(qū)域化學(xué)成分不均勻性,但不同點在于宏觀偏析一般側(cè)重于描述較大尺度范圍內(nèi)某一區(qū)域(如元素富集形成的偏析帶)與原始鋼水中的成分差異(如中心宏觀偏析);而大區(qū)域偏析元素分布不均勻度更傾向于描述較大尺度范圍內(nèi)所有位置的化學(xué)成分分布的不均勻性。
本文作者前期工作[17]針對高碳鋼鑄坯低倍組織灰度圖進(jìn)行研究,發(fā)現(xiàn)低倍組織灰度值與C含量存在較明顯的負(fù)相關(guān)關(guān)系,即灰度值越大,C含量越低。同時,利用標(biāo)準(zhǔn)熱鹽酸酸蝕實驗所得到的低倍組織灰度圖,易近似獲得大區(qū)域范圍內(nèi)C含量分布,從而為分析不同組織區(qū)域內(nèi)C元素分布不均勻度提供基礎(chǔ)。雖然低倍組織不同位置灰度值可能并不能完全準(zhǔn)確表示高碳鋼中主要偏析元素(C元素)的含量,但基于實際低倍組織灰度圖的分析可一定程度上客觀地反映C含量的不均勻分布特征;并且可以根據(jù)低倍組織灰度圖尺寸方便且靈活地實現(xiàn)不同范圍大區(qū)域的C元素分布不均勻度表征。另外,基于灰度圖進(jìn)行研究,目前已被應(yīng)用于材料研究的相關(guān)領(lǐng)域,例如估計金屬的腐蝕程度[18]、定量金相分析[19]和金屬表面缺陷檢測[20,21]等。但是,將高碳鋼鑄坯低倍組織灰度圖應(yīng)用于C元素分布不均勻度的研究還鮮見報道。
本工作以含C量為0.7% (質(zhì)量分?jǐn)?shù))的高碳鋼連鑄方坯為例,嘗試通過鑄坯低倍組織灰度圖探討一種簡易且系統(tǒng)表征高碳鋼鑄坯大區(qū)域C元素分布不均勻度的有效方法。首先,基于低倍組織灰度圖,采用標(biāo)準(zhǔn)差(standard deviation)、差分盒維數(shù)(differential box-counting)以及慣性矩(moment of inertia)來綜合定量表征鑄坯大區(qū)域C元素分布的不均勻度;然后,結(jié)合統(tǒng)計均勻度和近平衡凝固模型對C元素分布不均勻度表征結(jié)果的有效性進(jìn)行驗證;最后,探討3種表征方法的異同。
本實驗采用尺寸為170 mm × 170 mm的70鋼連鑄方坯,其主要成分(質(zhì)量分?jǐn)?shù),%)為:C 0.7,Si 0.2,Mn 0.65,P 0.011,S 0.0023,F(xiàn)e余量。為了獲取鑄坯低倍組織灰度圖,從鑄坯中心縱斷面取樣并進(jìn)行標(biāo)準(zhǔn)熱酸洗實驗。熱酸洗實驗中酸液為容積比1∶1的工業(yè)鹽酸水溶液,酸蝕溫度60~80℃,酸蝕時間25 min。熱酸洗實驗后得到整體中心縱斷面低倍組織,然后根據(jù)圖1所示位置從鑄坯表面到中心依次選取6個尺寸為10 mm × 10 mm的小方格(1#~6#),在同樣光源條件下使用NVC4030型二維影像儀獲取每個小方格的低倍組織圖像。在得到原始的低倍組織圖像后,利用Matlab2018a將原始圖像轉(zhuǎn)換為灰度圖,灰度圖尺寸為256 px × 256 px。
圖1 鑄坯中心縱斷面取樣位置示意圖
Fig.1 Schematic of sampling location in the central plane of billet (unit: mm)
對于高碳鋼鑄坯大區(qū)域C元素分布不均勻度不同角度的定量表征,本工作從標(biāo)準(zhǔn)差、差分盒維數(shù)和慣性矩等方法展開。首先,灰度值標(biāo)準(zhǔn)差通過計算與平均灰度值的波動差值反映鑄坯C元素分布的整體平均不均勻度。其計算公式為[22]:
式中,St為標(biāo)準(zhǔn)差;zu為圖像灰度值的隨機(jī)變量;P(zu)為對應(yīng)區(qū)域中灰度值的像素分布概率(u = 0, 1, ..., L - 1);m為灰度圖的灰度均值;L為可區(qū)分的灰度級數(shù)。
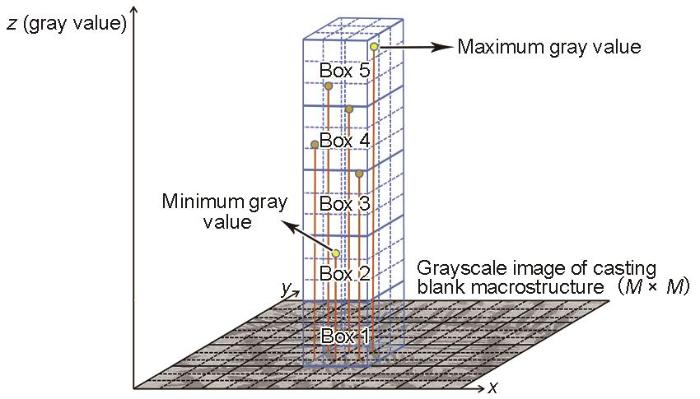
分形理論是研究大自然不規(guī)則復(fù)雜對象(例如三維形貌)的一種有效工具[23]。由于灰度圖像的灰度值分布是表面真實三維形貌的直接反應(yīng),因此基于表面灰度圖,分形理論已被應(yīng)用于各種材料表面三維形貌的定量表征,如材料磨損表面[24]、材料斷裂表面[25]和材料腐蝕形貌[26]等。分形維數(shù)作為分形的重要特征和度量,將圖像的空間信息和灰度信息簡單而有機(jī)地結(jié)合起來。分形理論的核心問題是如何準(zhǔn)確地估計分形維數(shù),前人已經(jīng)提出了一些計算灰度圖分形維數(shù)的方法[26],不同的計算方法從不同的角度對分形對象進(jìn)行描述,可以得到不同的分形維數(shù)值。其中由Sarkar和Chaudhuri[27]提出的差分盒維數(shù)具有動態(tài)取值穩(wěn)定和計算效率高等優(yōu)點,在計算灰度圖的分形維數(shù)被廣泛應(yīng)用,本工作也使用差分盒維數(shù)計算鑄坯組織灰度圖的分形維數(shù)。其基本原理為:對于給定區(qū)域為M × M的圖像,假設(shè)它己被分解成S × S的小塊,S是介于1~M/2之間的一個整數(shù)。此時尺度因子r = S / M。可把M × M的灰度圖像看成是一個三維空間,(x, y)表示各點的平面位置,第三維用來表示像素點的灰度值。當(dāng)把圖像平面劃分成若干S × S的網(wǎng)格,把第三維圖像的灰度值劃分成長度為S'的小段,則在每一個網(wǎng)格上存在一系列尺寸為S × S × S'的小盒子。設(shè)圖像的灰度級為L,取S'滿足[L / S'] = [M / S] = l / r。例如,如圖2所示,S = S' = 3,組織灰度圖平面的第(i, j)個網(wǎng)格內(nèi)灰度值最高和最低的像素點分別落在第5和第2個盒子,則覆蓋這個網(wǎng)格需要3個盒子。假設(shè)在圖像的第(i, j)個網(wǎng)格內(nèi)灰度值最高和最低的像素點分別落在第h和第k個盒子內(nèi),則尺度因子為r時的總盒子數(shù)N(r)在第(i, j)個網(wǎng)格內(nèi)的分布nr (i, j)由
圖2 差分盒維數(shù)算法示意圖
Fig.2 Schematic of differential box-counting algorithm (The size of a box is 3 × 3 × 3, which is used to cover gray value)
對所有的網(wǎng)格計算其分布,得到:
對應(yīng)于不同的r,可以得到不同的N(r)值。由分形維數(shù)的計算方法,采用最小二乘法擬合出lnN(r)-ln(1/r)的斜率,即為對應(yīng)的鑄坯組織灰度圖的差分盒維數(shù)(D),計算公式如下:
根據(jù)差分盒維數(shù)的計算原理可知,差分盒維數(shù)通過不同尺度下(局部到整體)的灰度最大值與最小值之差反映C元素分布不均勻程度。同時分形維數(shù)作為具有自相似性和無標(biāo)度性特征的表征參數(shù),具有尺度獨立性[26]。
Haralick等[28]在20世紀(jì)70年代初期提出的灰度共生矩陣(GLCM)是用來分析圖像紋理特征的經(jīng)典二階統(tǒng)計法,其反映圖像紋理關(guān)于方向、相鄰間隔、變化幅度的綜合信息,目前已被應(yīng)用于材料研究的許多相關(guān)領(lǐng)域,例如金屬形貌特征提取[29,30]和斷口形貌分析[25]等。灰度共生矩陣的基本原理是:取M × M的圖像灰度值為i的像素點(x, y)及偏離它的另一點灰度值為j的像素點(x + a, y + b),其中,a、b分別為兩像素點間的水平距離和垂直距離。若(x, y)與(x + a, y + b)間距為d,2者與坐標(biāo)橫軸的的夾角為θ,統(tǒng)計(i, j)同時出現(xiàn)的頻率,記為Pδ (i, j)。其中δ為i與j的某個固定位置關(guān)系(d, θ),i、j = 0, 1, 2, ..., n-1, n表示灰度值,稱由Pδ (i, j)組成的矩陣為灰度共生矩陣。通過灰度共生矩陣可以分析圖像灰度值分布的局部模式和排列規(guī)則,但一般不直接應(yīng)用得到的共生矩陣,而是在此基礎(chǔ)上獲取特征參數(shù),灰度共生矩陣特征參數(shù)慣性矩度量圖像的局部灰度值變化總量,可以作為衡量灰度值局部分布不均勻程度的指標(biāo)。慣性矩(CON)的計算公式為:
式中,(i, j)為圖像上灰度值為i和j的組合。
根據(jù)熱鹽酸酸蝕原理,酸液與高碳鋼鑄坯接觸發(fā)生反應(yīng)時,偏析區(qū)域C含量高其Gibbs自由能大,導(dǎo)致與酸液反應(yīng)劇烈且顏色變暗,即可通過鑄坯低倍組織灰度圖中的亮暗區(qū)域區(qū)分偏析與凝固組織[31]。根據(jù)實際生產(chǎn)現(xiàn)場廣泛使用的標(biāo)準(zhǔn)熱鹽酸酸蝕實驗,易得到鑄坯大區(qū)域范圍的低倍組織灰度圖,如圖3所示。從鑄坯表面向中心凝固組織呈現(xiàn)不同形貌,即從柱狀晶向等軸晶逐漸轉(zhuǎn)變,其中1#~3# (圖3a~c)位置主要為柱狀晶形貌,4#~6# (圖3d~f)位置主要為等軸晶形貌。根據(jù)GB/T 226-1991《鋼的低倍組織及缺陷酸蝕檢驗法》與前期研究[17,31],圖中灰度值較大的部分(亮度較高)為凝固組織,灰度值較低的部分(亮度較暗)為偏析區(qū)域;且灰度值與C含量近似呈現(xiàn)較好的負(fù)相關(guān)關(guān)系。故接下來將利用低倍組織灰度圖來分析鑄坯大區(qū)域C元素分布不均勻度變化。
圖3 鑄坯不同位置的低倍組織灰度圖
Fig.3 Grayscale images of macrostructures of samples 1#-6# at different locations of billet (a-f)
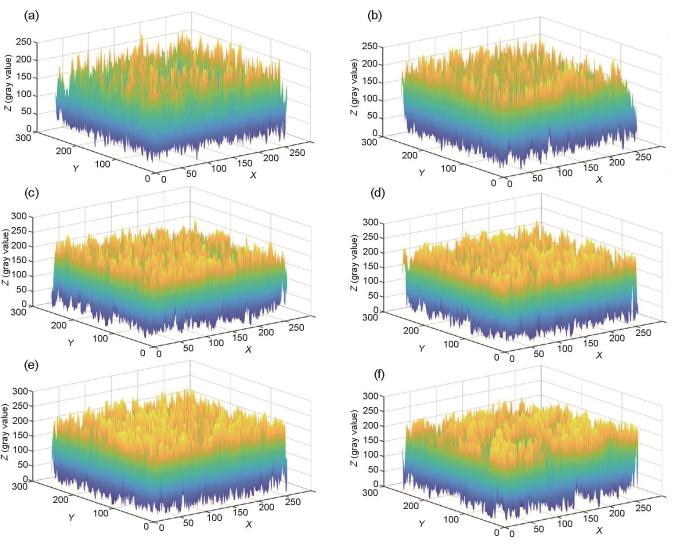
使用Matlab2018a編程繪制鑄坯不同位置低倍組織灰度圖的灰度曲面,即把灰度圖放置在XOY平面上,像素的灰度值作為Z軸上的值,由此構(gòu)成的曲面叫做圖像的灰度曲面,灰度曲面即近似為鑄坯C元素含量的空間分布。圖4為鑄坯內(nèi)部不同位置的低倍組織灰度曲面。可以看出,每個位置的低倍組織灰度曲面無論從整體或局部進(jìn)行觀察,均可以看出灰度值分布非常不均勻。由于灰度值分布不均勻是鑄坯C元素含量分布不均勻的一種表現(xiàn),故可以利用高碳鋼低倍組織灰度圖這種簡易方法來定性比較不同位置不均勻度的差別,但分布不均勻現(xiàn)象非常復(fù)雜,僅憑借定性觀察很難對比不同位置灰度值分布的不均勻程度。因此很有必要借助于上述方法準(zhǔn)確定量表征鑄坯不同位置灰度值分布不均勻度的不同方面,并以此來研究高碳鋼鑄坯大區(qū)域C元素分布不均勻度。
圖4 鑄坯不同位置的低倍組織灰度曲面
Fig.4 Grayscale surfaces of macrostructures of samples 1#-6# at different locations of billet (a-f) (The unit of X and Y axes is pixel)
圖5為鑄坯不同位置的灰度值標(biāo)準(zhǔn)差變化。可見,從鑄坯表面到中心,灰度值標(biāo)準(zhǔn)差逐漸增大;同時灰度值標(biāo)準(zhǔn)差在柱狀晶區(qū)(1#~3#)和等軸晶區(qū)(4#~6#)變化趨勢一致,但柱狀晶區(qū)灰度值標(biāo)準(zhǔn)差增長幅度更大,等軸晶區(qū)增長幅度較為平緩。圖3中從鑄坯表面到中心凝固組織形貌依次為柱狀晶和等軸晶。灰度值標(biāo)準(zhǔn)差通過衡量選定區(qū)域內(nèi)灰度值與平均灰度值的波動差值表征C元素分布整體平均不均勻度。因此,等軸晶區(qū)C元素分布整體平均不均勻度相較于柱狀晶區(qū)更高。同時,通過計算等軸晶區(qū)和柱狀晶區(qū)標(biāo)準(zhǔn)差均值之差與柱狀晶區(qū)標(biāo)準(zhǔn)差均值的比值可知,等軸晶區(qū)C元素分布整體平均不均勻度比柱狀晶區(qū)高25.38%。
圖5 鑄坯不同位置的灰度值標(biāo)準(zhǔn)差
Fig.5 Standard deviation of grayscale value at different locations of billet
根據(jù)差分盒維數(shù)的計算原理,使用Matlab2018a編程對鑄坯不同位置的低倍組織灰度圖的差分盒維數(shù)進(jìn)行計算。圖6所示為鑄坯低倍組織1#試樣的lnN(r)-ln(1 / r)擬合關(guān)系。圖中分布點擬合直線的斜率為2.6177,擬合系數(shù)R2為0.9946。根據(jù)差分盒維數(shù)的計算原理可知,1#試樣的低倍組織灰度圖的差分盒維數(shù)是其擬合直線的斜率,即2.6177。根據(jù)同樣的方法可以得到鑄坯不同位置的低倍組織灰度圖差分盒維數(shù)及對應(yīng)的擬合系數(shù),具體數(shù)值見圖7和表1。可以看出,鑄坯不同位置的擬合系數(shù)均接近1,這表明低倍組織灰度圖具有很好的分形特征,引入差分盒維數(shù)這種方法來定量描述鑄坯不同位置灰度值分布特征是有效的。差分盒維數(shù)通過不同尺度下的灰度最大值與最小值之差反映不同尺度下的C元素分布不均勻程度。對于圖像的灰度分布曲面,差分盒維數(shù)介于2~3之間[27]。差分盒維數(shù)越接近于2,灰度分布曲面越光滑;差分盒維數(shù)越接近3,灰度分布曲面越粗糙。因此,當(dāng)差分盒維數(shù)越大時,代表此位置不同尺度下的C元素分布不均勻程度越大,即此位置從局部到整體C元素分布不均勻程度越大。
圖6 鑄坯低倍組織1#試樣lnN(r)-ln(1 / r)關(guān)系
Fig.6 Relationship between lnN(r) and ln(1 / r) of 1# sample (R2—fitting coefficients, r—size coefficient, N(r)—number of total boxes)
圖7 鑄坯不同位置的差分盒維數(shù)(D)
Fig.7 Differential box-counting (D) at different locations of billet
表1 不同位置的低倍組織灰度圖的D及對應(yīng)的擬合系數(shù)(R2)
Table 1
圖7為鑄坯不同位置的組織灰度圖的差分盒維數(shù)變化。可見,從鑄坯表面到中心組織灰度圖差分盒維數(shù)先逐漸增大,而后在中心等軸晶區(qū)發(fā)生波動。圖3中從鑄坯表面到中心凝固組織形貌依次為柱狀晶和等軸晶。差分盒維數(shù)在柱狀晶區(qū)(1#~3#)逐漸增大,在等軸晶區(qū)(4#~6#)存在波動。差分盒維數(shù)可以定量表征不同尺度下的C元素分布不均勻程度。因此,等軸晶區(qū)不同尺度下C元素分布不均勻程度相較于柱狀晶區(qū)更高。同時,通過計算等軸晶區(qū)和柱狀晶區(qū)差分盒維數(shù)均值之差與柱狀晶區(qū)差分盒維數(shù)均值的比值可知,等軸晶區(qū)不同尺度下C元素分布不均勻程度比柱狀晶區(qū)高1.57%。
本工作主要通過慣性矩定量表征微區(qū)C元素分布不均勻度,其中,間距d取1,夾角θ分別為0°、45°、90°、135°構(gòu)建灰度共生矩陣,并且以慣性矩均值作為衡量微區(qū)C元素分布不均勻度。圖8為慣性矩表征局部微區(qū)C元素分布不均勻度示意圖。可見,所構(gòu)建微區(qū)對應(yīng)的組織灰度值分布,即為3 × 3的灰度值矩陣。根據(jù)慣性矩的計算
圖8 慣性矩表征微區(qū)C元素分布不均勻度示意圖
Fig.8 Schematic of the nonuniformity of carbon micro distribution characterized by moment of inertia (d, θ—distance and angle between i and j, respectively )
圖9為鑄坯不同位置的組織灰度圖慣性矩變化。可見,從鑄坯表面到中心,慣性矩先逐漸增大,而后在中心等軸晶區(qū)發(fā)生波動。圖3中從鑄坯表面到中心凝固組織形貌依次為柱狀晶和等軸晶。因此,慣性矩在柱狀晶區(qū)(1#~3#)逐漸增大,在等軸晶區(qū)(4#~6#)存在波動。慣性矩定量表征微區(qū)C元素分布不均勻度。因此,等軸晶區(qū)C元素分布不均勻程度相較于柱狀晶區(qū)更高。同時,通過計算等軸晶區(qū)和柱狀晶區(qū)慣性矩均值之差與柱狀晶區(qū)慣性矩均值的比值可知,等軸晶區(qū)微區(qū)C元素分布不均勻度相較于柱狀晶區(qū)高35.61%。
圖9 鑄坯不同位置的慣性矩
Fig.9 Moment of inertia at different locations of billet
灰度直方圖是將低倍組織灰度圖的所有像素,按照灰度值的大小,統(tǒng)計其出現(xiàn)的頻數(shù)。低倍組織灰度圖可以近似代表區(qū)域內(nèi)C元素空間分布趨勢,因此灰度直方圖可以認(rèn)為是關(guān)于C元素分布的函數(shù),是對區(qū)域內(nèi)C元素分布的統(tǒng)計。
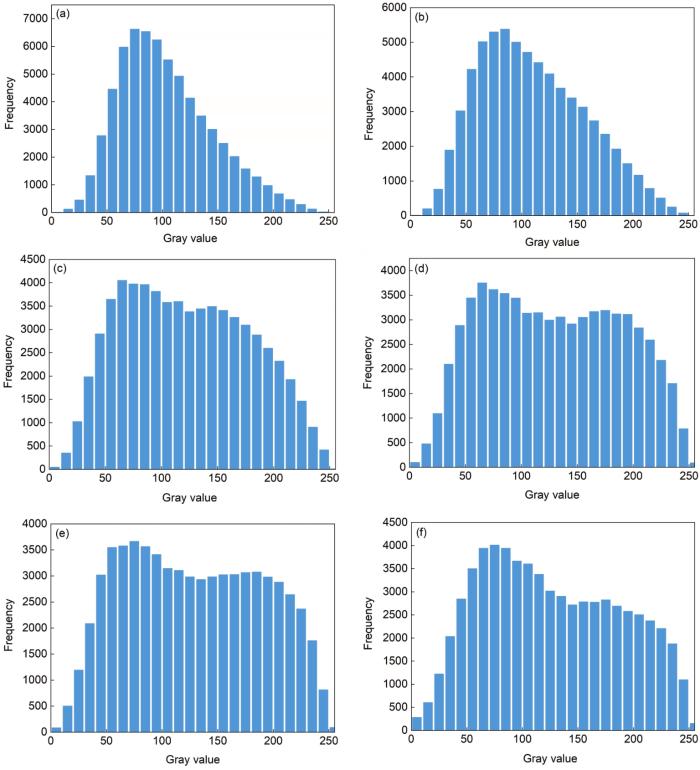
圖10為鑄坯不同位置的灰度直方圖。可見,1#、2#位置的灰度直方圖,其峰型較窄,說明C元素含量分布較為集中,表明這2個位置的C元素分布比較均勻;而對于3#~6#位置處的灰度直方圖,峰型較寬,說明C元素含量分布較為分散,則表示C元素分布比較不均勻。通過不同位置的灰度直方圖可以較為直觀地衡量不同位置C元素分布不均勻度。根據(jù)王海舟等[32]提出的連鑄坯原位統(tǒng)計分布的分析研究,通過對各原位置元素成分的權(quán)重比率統(tǒng)計分布進(jìn)行解析,可得到某元素在特定含量區(qū)間(如允許差范圍內(nèi))所占的權(quán)重比率(或稱所占的頻率),用以定量表征其統(tǒng)計均勻度(H),反映大區(qū)域內(nèi)元素定量統(tǒng)計分布規(guī)律,其數(shù)值越大,表明在此材料中該元素分布的均勻性越好。H即為在元素平均含量的國家標(biāo)準(zhǔn)規(guī)定允許差范圍內(nèi)所占頻率。根據(jù)GB/T 222-2006《鋼的成品化學(xué)成分允許偏差》可知,70鋼C含量允許差范圍為0.7% ± 0.04%。灰度直方圖可以代表鑄坯各位置C元素含量的權(quán)重比率統(tǒng)計分布,因此可以以鑄坯不同位置的灰度值均值g0作為C元素平均含量,根據(jù)70鋼C含量允許差范圍計算出對應(yīng)灰度值允許差范圍為(1 ± 5.714%)g0,然后計算出H。表2為鑄坯不同位置的灰度值允許差范圍和H。可見,1#~3#位置的統(tǒng)計均勻度較明顯大于4#~6#。圖3中從鑄坯表面到中心凝固組織形貌依次為柱狀晶和等軸晶,因此,等軸晶的C元素分布不均勻度大于柱狀晶區(qū)。同時,圖11分別為統(tǒng)計均勻度隨標(biāo)準(zhǔn)差、差分盒維數(shù)以及慣性矩的變化。可見,隨著標(biāo)準(zhǔn)差、差分盒維數(shù)、慣性矩的增加,統(tǒng)計均勻度均明顯減小。
圖10 鑄坯不同位置的灰度直方圖
Fig.10 Gray histograms of samples 1#-6# at different locations of billet (a-f)
表2 灰度值在含量允許差范圍內(nèi)所占的權(quán)重比率(統(tǒng)計均勻度(H))
Table 2
Grayscale value in the range
of content tolerance
圖11 統(tǒng)計均勻度與標(biāo)準(zhǔn)差、差分盒維數(shù)、慣性矩的關(guān)系
Fig.11 Relationship between H and standard deviation (a), differential box-counting (b), and moment of inertia (c)
以上表明,標(biāo)準(zhǔn)差、差分盒維數(shù)和慣性矩的表征結(jié)果與統(tǒng)計均勻度計算方法的結(jié)果是基本一致的。但與此同時,圖11并沒有呈現(xiàn)出完全負(fù)相關(guān)的關(guān)系,這表明本工作所提出的3種表征方法對不均勻度從不同角度進(jìn)行了更為精細(xì)化的表達(dá)。
連鑄坯在凝固過程中溶質(zhì)元素分布除了受到溫度梯度、濃度梯度、凝固組織、液相流動等方面的影響,更主要的是受到凝固過程固/液界面溶質(zhì)再分配的影響。因此,為了有效描述高碳鋼鑄坯從表面到中心不同位置溶質(zhì)元素再分布,可通過偏析元素固相無擴(kuò)散且液相有限擴(kuò)散的近平衡凝固模型[33~35]對其凝固過程進(jìn)行分析。Burton等[35]提出近平衡凝固過程中固/液界面處的溶質(zhì)有效分配系數(shù)(kE)可用
式中,DL是溶質(zhì)擴(kuò)散系數(shù);C0是合金的原始成分;k0是溶質(zhì)平衡分配系數(shù);C
式中,fs是固相體積分?jǐn)?shù);CL是固/液界面液相中C的質(zhì)量分?jǐn)?shù)。
從
圖12為不同kE時CL與fs的關(guān)系。可見,隨著fs的增加,CL呈指數(shù)遞增;同時,kE越小,CL由小到大變化的劇烈程度(切線斜率)越大,也即CL波動越大,導(dǎo)致C元素分布不均勻程度增加;另外,kE越小,CL越大,導(dǎo)致偏析程度增加。當(dāng)凝固由外往內(nèi)逐漸發(fā)生時,kE逐漸減小,從而C元素分布不均勻程度和偏析程度整體均呈現(xiàn)遞增趨勢;且C元素分布不均勻度越大,對應(yīng)區(qū)域內(nèi)偏析程度越嚴(yán)重。圖3中從鑄坯表面到中心凝固組織形貌依次為柱狀晶區(qū)和等軸晶區(qū),因此,本工作70高碳鋼連鑄坯中等軸晶區(qū)的C元素分布不均勻度相對于柱狀晶區(qū)更高;且基于標(biāo)準(zhǔn)差、慣性矩和差分盒維數(shù)的計算結(jié)果,其不均勻度相差比例的平均值為20.85%。
圖12 液相中C的質(zhì)量分?jǐn)?shù)(CL)與固相體積分?jǐn)?shù)(fs)的關(guān)系
Fig.12 Relationship between mass fraction of carbon in the liquid phase (CL) and solid fraction (fs) (kE—effective distribution coefficient of solute)
上述研究表明,標(biāo)準(zhǔn)差、慣性矩和差分盒維數(shù)都能有效地反映大區(qū)域C元素分布不均勻度,以及鑄坯從表面向中心凝固過程中不均勻度變化的整體趨勢。根據(jù)3種方法的原理和計算方法可知,標(biāo)準(zhǔn)差是基于低倍組織灰度圖上所有灰度值與灰度均值的統(tǒng)計特性計算得出的結(jié)果;差分盒維數(shù)和慣性矩結(jié)合了低倍組織灰度圖上灰度值統(tǒng)計信息和空間分布信息,但前者只計算不同尺度下的灰度最大值和最小值,而舍棄了其他灰度值數(shù)據(jù),導(dǎo)致?lián)p失了許多灰度值信息,可能使不同位置的差分盒維數(shù)計算結(jié)果不敏感;而后者的計算則充分利用了灰度圖上所有灰度值信息,對計算結(jié)果會更加敏感。另外,相對于標(biāo)準(zhǔn)差和慣性矩,差分盒維數(shù)具有尺度獨立性,受灰度圖尺寸和分辨率的影響較小。從3種方法的整體變化趨勢來看,鑄坯不同位置的慣性矩和差分盒維數(shù)雖然變化趨勢相同,但變化程度存在很大差別。可通過計算表征參數(shù)最大值與最小值之差與平均值之比作為定量比較差分盒維數(shù)與慣性矩的整體變化程度。相較于平均值來說,差分盒維數(shù)的整體變化程度很小,僅有3.6%,而慣性矩的變化程度達(dá)到了68.7%。因此,慣性矩的變化相對于差分盒維數(shù)更加敏感。標(biāo)準(zhǔn)差、差分盒維數(shù)和慣性矩均表明等軸晶區(qū)C元素分布不均勻度相較于柱狀晶區(qū)更高,但相差程度存在較大差別,其中等軸晶區(qū)標(biāo)準(zhǔn)差比柱狀晶區(qū)高25.38%;差分盒維數(shù)比柱狀晶區(qū)高1.57%;慣性矩比柱狀晶區(qū)高35.61%。
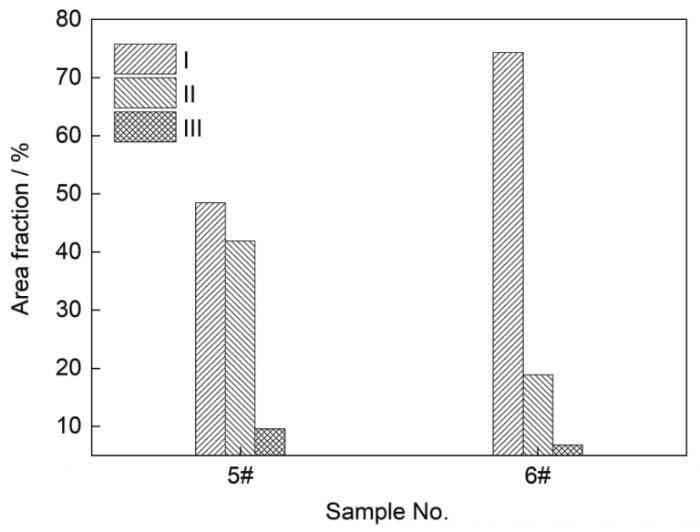
同時,通過圖5、7和9可以看出,慣性矩與差分盒維數(shù)在5#到6#位置處的變化趨勢與標(biāo)準(zhǔn)差存在差別。從5#到6#位置,標(biāo)準(zhǔn)差增大,差分盒維數(shù)和慣性矩降低。在分析過程中也發(fā)現(xiàn),鑄坯同一位置的碳偏析點尺寸不同,因此本工作基于偏析點的尺寸將偏析點分為I、II、III 3種類型。3種類型對應(yīng)的偏析點面積分別為:> 1 mm2、0.1~1 mm2、< 0.1 mm2。根據(jù)實際鑄坯的偏析程度,本研究把 I 類歸為大型偏析點,II類歸為中型偏析點,III 類歸為小型偏析點。根據(jù)偏析點的尺寸,可由此計算不同類型偏析點面積比(不同類型偏析點面積與偏析點總面積之比)。圖13為5#和6#位置處的I、II、III 3類偏析點的面積比。可以看出,I和II類偏析點面積比變化劇烈,III類偏析點面積比變化程度接近。其中,6#相對5#位置,I類碳偏析點面積比增加25.82%,II類偏析點面積比減小23.03%。5#到6#位置,標(biāo)準(zhǔn)差增大,表明標(biāo)準(zhǔn)差可以作為衡量I類偏析點面積比的指標(biāo),即標(biāo)準(zhǔn)差越大,對應(yīng)區(qū)域內(nèi)I類偏析點面積比越大。相反,5#到6#位置,差分盒維數(shù)和慣性矩降低。表明差分盒維數(shù)和慣性矩可以作為衡量II類偏析點面積比的指標(biāo),即差分盒維數(shù)和慣性矩越大,對應(yīng)區(qū)域內(nèi)II類偏析點面積比越大。另外,I類偏析點面積比越大或II類偏析點面積比越大均可能造成鑄坯后續(xù)熱處理均勻化的難度增加。
圖13 5#、6#位置I、II、III 3類偏析點的面積比
Fig.13 Area ratios of I, II, and III three kinds of segregation points (5#-6#)
綜上所述,標(biāo)準(zhǔn)差、差分盒維數(shù)和慣性矩從不同角度定量表征C元素分布不均勻度,3種方法的變化趨勢、變化程度以及等軸晶區(qū)與柱狀晶區(qū)C元素分布不均勻度之差均存在不同差別;同時標(biāo)準(zhǔn)差可以作為衡量I類偏析點面積比的指標(biāo),差分盒維數(shù)和慣性矩可以作為衡量II類偏析點面積比的指標(biāo)。因此,對于高碳鋼鑄坯大區(qū)域C元素分布不均勻度的全面衡量可考慮3種表征方法結(jié)合使用,從而實現(xiàn)對C元素分布不均勻度的綜合評價。
(1) 針對定量表征高碳鋼鑄坯大區(qū)域C元素分布不均勻度的不足,基于鑄坯低倍組織灰度圖,可利用標(biāo)準(zhǔn)差、差分盒維數(shù)和慣性矩分別從整體平均不均勻度、不同尺度下的不均勻度和局部不均勻度等角度對C元素分布不均勻度進(jìn)行綜合有效表達(dá)。
(2) 由連鑄坯外部柱狀晶區(qū)至內(nèi)部等軸晶區(qū),C元素分布不均勻度整體呈逐漸增加的趨勢,且等軸晶區(qū)C元素分布不均勻度均值相對柱狀晶區(qū)高20.85%。
(3) 標(biāo)準(zhǔn)差主要基于灰度值統(tǒng)計特性,差分盒維數(shù)和慣性矩結(jié)合了低倍組織灰度圖上灰度值統(tǒng)計信息和空間分布信息;并且差分盒維數(shù)具有尺度獨立性,受灰度圖尺寸和分辨率的影響較小,而慣性矩對微區(qū)C元素分布不均勻度變化會更加敏感。此外,標(biāo)準(zhǔn)差主要受大型偏析點(> 1 mm2)影響,而差分盒維數(shù)和慣性矩主要受中型偏析點(0.1~1 mm2)影響。對于高碳鋼鑄坯大區(qū)域C元素分布不均勻度的全面衡量可考慮3種表征方法結(jié)合使用。
1 實驗方法
圖1
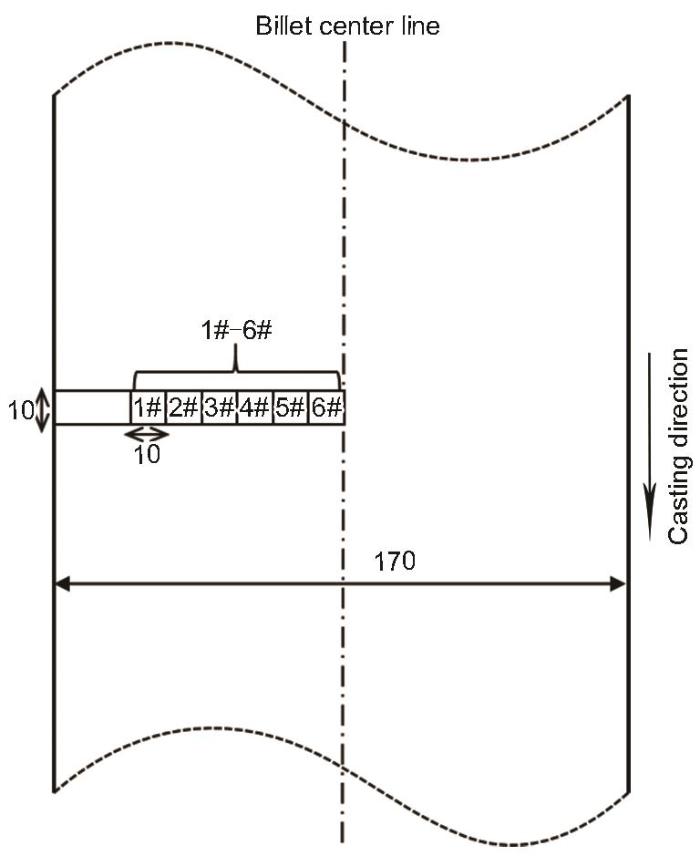
圖2
2 實驗結(jié)果與討論
2.1 低倍組織灰度圖
圖3

圖4
2.2 C元素分布不均勻度表征結(jié)果
2.2.1 標(biāo)準(zhǔn)差
圖5

2.2.2 差分盒維數(shù)
圖6

圖7

Sample No.
D
R2
1#
2.6177
0.9946
2#
2.6622
0.9950
3#
2.6786
0.9946
4#
2.6820
0.9943
5#
2.7140
0.9946
6#
2.6791
0.9946
2.2.3 慣性矩
圖8

圖9

2.3 C元素分布不均勻度表征結(jié)果有效性討論
圖10
Sample No.
H / %
1#
11.98
[97,110]
2#
9.76
[103,116]
3#
8.39
[115,130]
4#
7.35
[121,136]
5#
6.02
[121,136]
6#
7.33
[118,133]
圖11
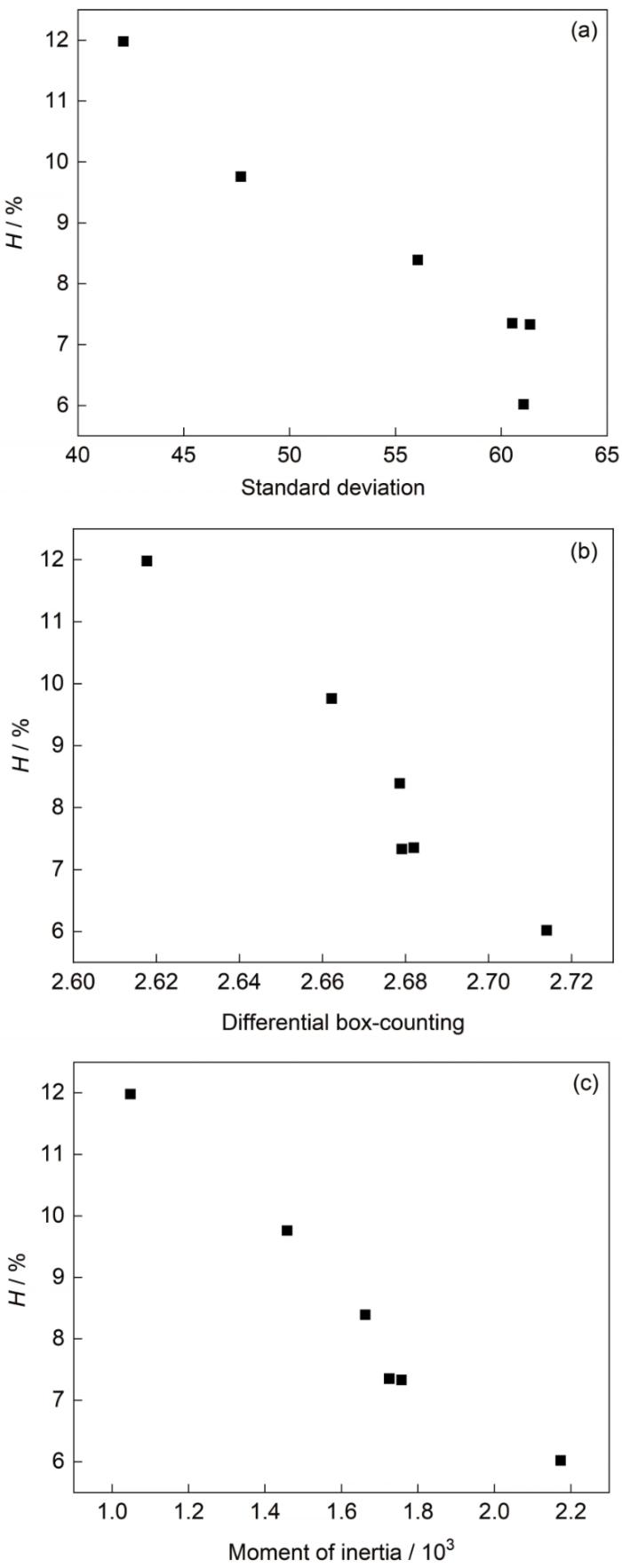
圖12

2.4 標(biāo)準(zhǔn)差、差分盒維數(shù)和慣性矩的對比討論
圖13
3 結(jié)論
來源--金屬學(xué)報







 滬公網(wǎng)安備31011202020290號
滬公網(wǎng)安備31011202020290號
