分享:鐵素體-貝氏體雙相鋼韌性斷裂過程中的夾雜物臨界尺寸及孔洞生長
趙亞峰1,2, 劉蘇杰1, 陳云1, 馬會1, 馬廣財3, 郭翼 ,1
,1
1
2
3
利用多模態(tài)關聯(lián)成像方法研究了鐵素體-貝氏體雙相鋼韌性斷裂過程中局部微結構對孔洞生長的影響。首先使用X射線CT成像技術,從宏觀層面量化分析了變形過程中孔洞的生長,并定位典型孔洞的空間坐標。之后對選定的目標孔洞,采用等離子體聚焦離子束(PFIB)進行連續(xù)切片三維電子背散射衍射(3D-EBSD)掃描成像,從介觀層面研究孔洞周圍微觀組織對孔洞形核與生長的影響。結果顯示,夾雜物周圍和貝氏體中均有孔洞形成。盡管有時促使大尺寸孔洞生長的應變比小尺寸孔洞處的應變更小,但相比于在小尺寸夾雜物或貝氏體中形核的孔洞,大尺寸夾雜物導致的孔洞體積更大。進一步對孔洞周圍的位錯密度研究顯示,上述現(xiàn)象可能是由于不同尺寸的夾雜物周圍應變梯度不同造成的。孔洞周圍的位錯密度與誘發(fā)孔洞的夾雜物尺寸成反比,存在明顯的尺寸效應,表明影響孔洞生長的夾雜物存在一個臨界尺寸。利用解析理論模型推測出夾雜物臨界尺寸范圍為1.85~2.86 µm,小于該臨界尺寸的夾雜物誘發(fā)的孔洞,由于局部變形梯度效應,位錯塞積會阻礙孔洞的生長。孔洞的生長是非均勻的且其形狀表現(xiàn)出各向異性,孔洞生長形貌與周圍晶粒的可變形性相關,可用晶粒尺寸加權的Schmid因子描述。
關鍵詞:
由于雙相鋼的生產規(guī)模大、成本低、易于加工,在保持高強度的同時保持了良好的塑性和韌性[1],所以在汽車行業(yè)中被廣泛使用[2]。雙相鋼通常具有類似復合材料的微觀結構:在軟的鐵素體基體上分布著硬的第二相組織,如馬氏體、亞穩(wěn)奧氏體或貝氏體等。在變形過程中,軟的鐵素體基體容易發(fā)生變形使其具有好的塑性,硬的第二相又保證了強度的要求。材料韌性斷裂的一個關鍵物理過程是孔洞的形核、生長和聚合,諸多研究者發(fā)現(xiàn),在雙相鋼的鐵素體-馬氏體界面上觀察到孔洞形核是通過相界面的分離或第二相在中高應變條件下斷裂形成的[3,4],而在低應變條件下,孔洞可以在夾雜物的界面上較早形核[4]。大量的雙相鋼斷裂行為研究表明,在這些雙相鋼中,夾雜物引起的損傷是一種重要的破壞機制[5~9],Al2O3和硫化物夾雜是重要的裂紋源[10],不過夾雜物孔洞的尺寸和形狀對Lode參數(shù)不敏感[11],僅與應力三軸度相關[12]。此外,與夾雜物有關的孔洞形核具有尺寸效應:與小顆粒相比,孔洞形核更易在大顆粒夾雜物上出現(xiàn)[5,6],減少大顆粒夾雜物的數(shù)量可以作為提高雙相鋼強度和塑性的一個設計準則。鋼的總塑性應變對孔洞的數(shù)量有較大的影響[13],研究孔洞在雙相鋼韌性斷裂過程中的形核和長大行為,有助于更好地認識孔洞在裂紋的萌生和擴展中的作用,以評估材料在服役過程中的損傷演化,同時,也為設計新鋼種和改進現(xiàn)有鋼種提供新的思路。
通常,孔洞在夾雜物上形核通過空位聚集、顆粒與基體界面分離或顆粒斷裂等機制實現(xiàn)。在高溫和低應變速率下,以空位聚集成孔洞的形核機制較為常見,這種機制多與蠕變相關[14]。有研究[6,15]表明,當形成孔洞的界面能小于基體表面能的0.1%時,較易發(fā)生空位聚集誘導的孔洞形核現(xiàn)象。對于機械變形引起的孔洞形核,顆粒斷裂和顆粒與基體界面的分離是2種相互競爭的機制。究竟哪種機制占主導地位,取決于顆粒與基體之間強度的差異[14]。一般來說,顆粒與基體強度差異較大時傾向于通過界面分離形成孔洞。此外,還有一些其他因素也會對這2種模式的競爭機制產生影響,例如顆粒的形狀和應力的大小,這是由于球形顆粒和較大的內應力會促進界面分離,實現(xiàn)孔洞形核所致[5]。
從微觀層面來看,常溫下孔洞的生長被認為是由剪切位錯環(huán)或柱面位錯環(huán)滑移產生的[16]。Bulatov等[17]對剪切環(huán)機制進行了詳細論證,結果表明,當一個完整的剪切環(huán)在孔洞表面形成時,孔洞將回復到原來的形狀,就是說剪切位錯環(huán)機制不能有效促進孔洞生長。另外,Gungor等[18]和Segurado等[19]通過分子動力學和位錯動力學模擬,證明了一對反平行位錯偶滑移也能夠促進孔洞的生長。
孔洞的聚合是形成微裂紋的重要機制,它可以通過下述一種或多種機制的協(xié)同產生[20,21]:(1) 局部頸縮:孔洞長大到一定程度之后相鄰孔洞之間的基體難以承受外加變形的載荷,因而產生局部化變形,最終導致相鄰孔洞之間的基體局部斷裂,孔洞在垂直于外部加載的方向上連接;(2) 局部剪切:與局部頸縮相似,這種模式也是由于局部塑性流變造成的,與(1)區(qū)別在于孔洞分布在與加載軸呈一定角度的方向上,特別是在45°最大剪切力下最易產生。此外,文獻[5]中還使用過一些諸如“void sheeting”和“necklace coalescence”等詞匯來描述孔洞沿剪切帶和晶界的聚合現(xiàn)象,但是都認為,孔洞聚合基本上取決于孔洞本身的生長動力學和孔洞間距[22]。
對于機械變形引起的夾雜物界面孔洞形核,Tanaka等[23]從應變能的角度計算了孔洞形核的臨界應變。假設形成無應變表面所需的能量高于新表面形成時顆粒弛豫的應變能,可將孔洞形核的臨界應變(εc)表示為[23]:
式中,k = E* / E,E*和E分別是顆粒和基體的Young's模量;β是一個取決于k以及顆粒和基體Poisson比的系數(shù);r是顆粒半徑。
Ashby[16]基于位錯應力場分析,提出了一種孔隙形核的應力模型。該模型認為夾雜物與基體彈性性質的差異是變形過程中形成柱面位錯環(huán)的主要原因,并且柱面位錯環(huán)在夾雜物與基體界面處的塞積會對界面施加一個拉應力,一旦這個拉應力超過界面的結合強度就會引起孔洞形核,且孔洞形核的臨界拉應力(σc)與顆粒直徑成正比,其形式為[16]:
式中,a是主滑移系的累積應變,d是顆粒直徑,l是位錯環(huán)的長度,b是Burgers矢量模。從
為了預測含孔洞塑性材料的流變行為,Gurson[24]提出了一種屈服準則,后經(jīng)Tvergaard和Needleman[25,26]修正,形成了著名的GTN塑性損傷模型。該模型將孔洞體積分數(shù)與基體材料的流變應力聯(lián)系起來,并假設基體在整個變形過程中的塑性變形是均勻分布的。實際上,由于應變梯度塑性效應以及孔隙周圍微織構的影響,顆粒與基體界面處的塑性變形與遠離界面的基體塑性變形可能存在較大的差異[6]。
本工作使用X射線CT成像(X-ray computed tomography,XCT) 技術[27~29],從宏觀層面研究鐵素體-貝氏體雙相鋼拉伸變形過程中夾雜物周圍的孔洞生長行為,并結合Xe+等離子體聚焦離子束(PFIB)在特定的位置取樣進行連續(xù)切片,開展三維電子背散射衍射(3D-EBSD)表征分析,在介觀層面研究了孔洞周圍組織結構對孔洞生長的影響。通過應變和位錯密度分析揭示了孔洞生長動力學的影響因素。此外,基于早期理論模型估算了受變形梯度塑性影響導致孔洞生長緩慢的夾雜物臨界尺寸,為高強鋼的夾雜物控制提供參考。
1 實驗方法
本工作所用鐵素體-貝氏體雙相鋼的主要化學成分(質量分數(shù),%)為:C 0.035,Si 0.30,Mn 1.51,P < 0.002,S < 0.001,Nb 0.046,V 0.051,F(xiàn)e余量,C當量為0.30。熱處理過程詳見參考文獻[30],熱處理后鋼中的貝氏體含量為10% (質量分數(shù))。
鐵素體-貝氏體雙相鋼通過線切割加工成棒狀拉伸試樣,長度為2.0 mm、直徑為1.1 mm,中心制備半徑為0.1 mm的圓形凹槽以提高應力三軸度。原位拉伸實驗使用放置在Versa 520 XCT設備中最高載荷5 kN的Deben CT5000拉伸試驗臺進行拉伸測試,應變速率約為8 × 10-4 s-1。拉伸應力達到抗拉強度(UTS)之后,在不同工程應變(ε = 0.038、0.047、0.049、0.05、0.053)狀態(tài)下和斷裂后進行CT掃描,以監(jiān)測應力達到UTS后不同應變狀態(tài)下的孔洞生長情況。每次CT掃描前將負載減少10%并靜置15 min,以減少掃描過程中圖像的漂移。XCT實驗使用110 kV下10 W的X射線源,在360°旋轉的過程中,采用多模態(tài)關聯(lián)成像方法共收集到1201張投影照片。每個照片曝光時間為75 s,使用4倍的物鏡采集,并進行2 × 2的像素合并,得到有效空間分辨率約為2.04 μm。使用Reconstructor軟件中的filtered back projection算法對實驗收集到的1201個投影進行三維體積重構,并使用Avizo軟件(ThermoFisher Scientific)進行可視化處理。在斷裂后的樣品上選取感興趣的孔洞,在其上方約50 μm的位置上沿軸向切割并拋光,運用Gemini SEM 460掃描電鏡(SEM)獲取截面像,并與相應位置處的XCT切片圖進行比較,以確認拋光后孔洞的次表層位置。接著使用Helios Xe+ PFIB[31]對體積為98 μm × 98 μm × 80 μm且包含預選孔洞的區(qū)域進行塊體挖掘,使用30 kV、0.18 μA的束流進行連續(xù)切片EBSD成像[32]。EBSD實驗參數(shù)為20 kV和22 nA,工作距離為10 mm,使用NordlysMax2系統(tǒng)和Aztec軟件收集衍射花樣,EBSD攝像頭增益設定為0,曝光時間為10 ms,使用4 × 4像素合并,采樣頻率為100 Hz、采樣步長為0.25 μm。在此參數(shù)設定下每個EBSD切片采樣大約需要16 min。由于樣品變形量較大,為提高EBSD衍射花樣質量,采用高曝光時間和低采樣頻率。3D-EBSD體積重建使用Dream3D (dream3d.bluequartz.net)開源軟件,為降低相鄰切片的錯配度,首先實現(xiàn)相鄰切片中晶粒之間的最大重疊來進行相鄰切片的對齊堆疊,接下來通過最小化每個切片中的像素點與其上下切片對應像素之間的取向差來進一步調整對齊。使用ParaView (paraview.org)開源軟件對3D-EBSD進行可視化處理。
2 實驗結果
2.1 孔洞的多尺度成像分析
圖1a~e為不同應變時XCT數(shù)據(jù)的二維切片圖,反映了達到UTS之后孔洞的形核、生長以及斷裂過程。可以看出,在ε達到0.05后孔洞加速形核,在ε達到0.053時,多數(shù)孔洞發(fā)生聚合,導致立即斷裂(圖1f)。從樣品中間的人字形裂縫(圖1f中黃色虛線框)可以看出,裂紋源是由局部剪切引起孔洞聚合后,兩側區(qū)域發(fā)生剪切失效形成特有的杯錐狀斷口,并在加載方向大致45°位置處形成剪切唇(圖1f中紅色虛線框)。圖1g和h為圖1e中所指不同位置的橫截面切片圖。從圖1g的橫向切片圖可以看出,大量的孔洞聚集在樣品截面的左側,這可能是由于左側缺口稍深,變形不均勻,從而產生了更多的孔洞所致,圖1h中的孔洞較少且分布很分散。圖1i為雙相鋼單向拉伸的應力-應變曲線。圖1a中所標定的2個孔洞從拉伸應力達到UTS后,裂紋開始形核,裂紋生長貫穿整個頸縮階段,直到斷裂,整個過程中沒有與其他孔洞合并。這種方法適合孔洞生長的局部組織結構環(huán)境影響的研究。
圖1

圖1 拉伸應力達到極限抗拉強度(UTS)后在不同工程應變(ε)水平下和斷裂后的XCT二維切片圖和單向拉伸應力-應變曲線
Fig.1 2D slice images of time-lap CT scans at different strain (ε) levels post ultimate tensile strength (UTS) (a-h) and stress-strain curve (i) (The rate of void nucleation increases rapidly between nominal strain of 0.05 and 0.053, which quickly coalesced and led to fracture)
Color online
(a) ε = 0.038 (b) ε = 0.047 (c) ε = 0.049
(d) ε = 0.05 (e) ε = 0.053 (f) fracture
(g) slice at the fracture surface before fracture in Fig.1e (h) slice at the region of interest shown in Fig.1e
通過橫截面直徑(D)計算出2個孔洞位置的真實應變(εT),εT = ln (
圖2
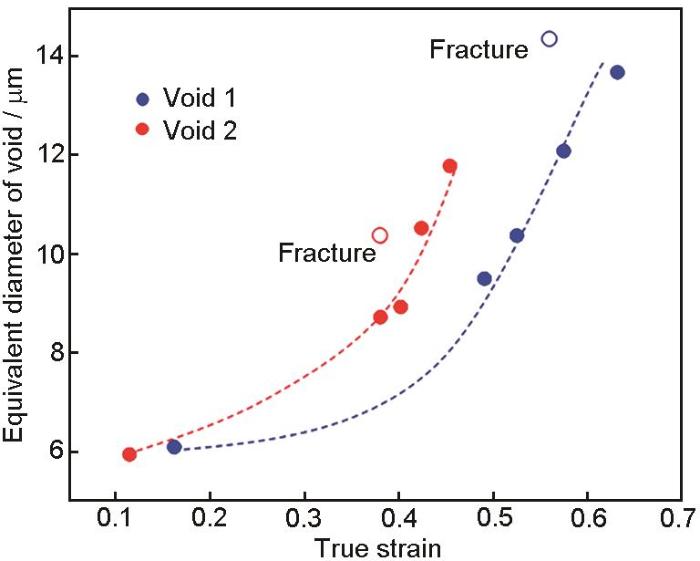
圖2 圖1a中2個孔洞的等效直徑與樣品相應截面上真實應變的關系
Fig.2 Equivalent diameters of two voids in Fig.1a as a function of true strain at the corresponding cross section of the sample (Each data point corresponds to a scan point marked in Fig.1i)
Color online
使用XCT、PFIB和EBSD技術詳細研究了2個孔洞附近的顯微組織,實驗過程如圖3所示。如圖3a所示,通過XCT確定孔洞的空間坐標,在此基礎上,對樣品進行切割和拋光,使孔洞位于拋光表面下約50 μm處,以方便后續(xù)實驗。使用PFIB對包含孔洞的區(qū)域整體挖掘(圖3b)并進行連續(xù)切片EBSD掃描(圖3c)。通過3D-EBSD掃描結果二維切片和三維統(tǒng)計的晶粒尺寸分布比較(圖3d)可以看出,三維分析的晶粒尺寸更接近正態(tài)分布,三維真實晶粒尺寸比二維截面晶粒尺寸平均高出3倍。這是由于在二維截面上計算的晶粒尺寸只能反映晶粒尺寸分布的下限,而一個界面橫跨截面上所有晶粒大圓的概率是極低的。圖4a顯示了圖1a中標注的2個孔洞和周圍晶粒的形態(tài)。可以看出,孔洞1位于晶界位置,而孔洞2完全被包裹在一個晶粒內,根據(jù)圖4b所示孔洞生長的位錯機制可以看出,孔洞2左右兩側的晶界限制了位錯滑移,導致與孔洞1相比,孔洞2在水平方向的尺寸較小,故整體形貌較為狹長。
圖3

圖3 研究孔洞生長的多模態(tài)關聯(lián)表征方法
Fig.3 Multimodal correlative approach to study void growth
Color online
(a) XCT morphology of the fractured sample, voids coloured in red
(b) bulk cut out by PFIB at the corresponding location indicated by circle in Fig.3a
(c) serial sectioning 3D-EBSD reconstruction (~98 μm × 98 μm × 80 μm) of the cutted bulk shown in Fig.3b
(d) comparisons between 2D and 3D grain size distributions
圖4
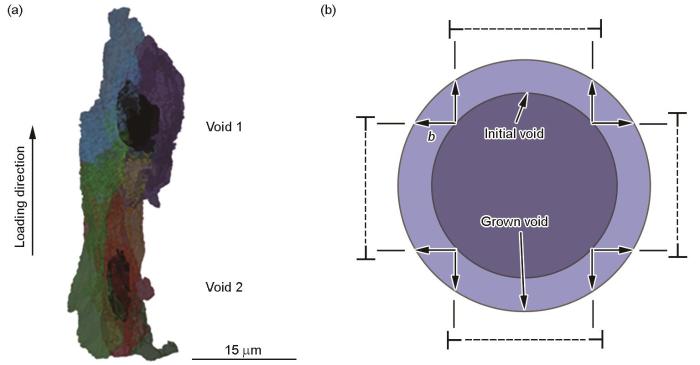
圖4 圖1a所示的2個孔洞及其周圍晶粒的XCT三維視圖,以及孔洞生長的位錯環(huán)機制示意圖
Fig.4 High resolution XCT morphology of the two voids shown in Fig.1a together with the grains surrounding the two voids (a), illustration demonstrating void expansion caused by glide of dislocation loops (b—Burgers vector module) (b)
Color online
2.2 孔洞形核點的微觀結構
所研究的鐵素體-貝氏體雙相鋼的顯微組織包括較軟的鐵素體基體和較硬的貝氏體相。貝氏體中C含量較高,故其內包含的位錯密度更高。圖5顯示了低應變和高應變區(qū)域顯微組織的EBSD像。貝氏體相由于較低的衍射花樣質量,在帶對比圖上較暗(圖5a~c)。這也可以通過EBSD標定的晶粒取向著色圖(圖5d~f)中的“碎晶”區(qū)識別。從變形后的EBSD像可以看出,晶粒沿水平拉伸方向伸長,雖然變形后貝氏體相仍然可以從鐵素體中分辨出來,但是高塑性變形形成的剪切帶和位錯胞的存在使兩相的界面難以嚴格確定。可以看出,2個大的孔洞是在夾雜物(Al2O3或MnS)周圍形成的,與貝氏體和貝氏體-鐵素體相界無直接關聯(lián)。
圖5
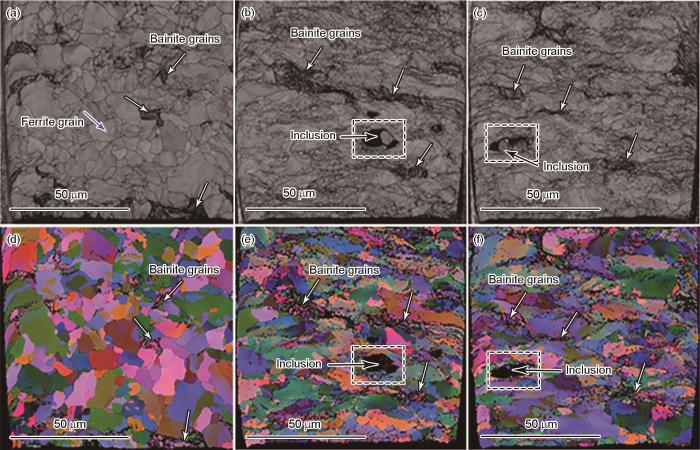
圖5 低應變區(qū)和包含孔洞1和孔洞2的中間截面高應變區(qū)域的EBSD帶對比圖和Euler角著色像
Fig.5 EBSD band contrast maps (a-c) and EBSD maps colored with Euler angles (d-f) in low strained region showing the un-deformed images (a, d) and high strained regions featuring the mid cross section of void 1 (b, e) and void 2 (c, f)
Color online
從3D-EBSD像(圖3c)可以發(fā)現(xiàn)大量低于XCT分辨率的小孔洞。可將這些孔洞大致分為3組:與貝氏體相關的孔洞(位于相界或內部,包括在貝氏體相內的夾雜物周圍出現(xiàn)的形核孔洞)、鐵素體中非夾雜物孔洞以及鐵素體內夾雜物周圍的孔洞,統(tǒng)計結果顯示在圖6中。可以看出,鐵素體中由夾雜物形核的孔洞尺寸大于在貝氏體中形核的孔洞尺寸。需要說明的是,大多數(shù)與貝氏體相關的孔洞周圍沒有觀察到夾雜物,有可能是夾雜物太小而無法分辨或是夾雜物在PFIB切片過程中脫落。將鐵素體中夾雜物尺寸和與之對應的孔洞尺寸進行對比,顯示2者呈正相關關系,如圖7所示。但是對孔洞位置的真實應變進行分析發(fā)現(xiàn),真實應變與孔洞尺寸的相關性較弱,如圖7中所示的尺寸在1.5~2 µm之間的夾雜物產生的孔洞相互之間真實應變差異巨大,但是孔洞尺寸卻十分接近,這表明孔洞的尺寸不僅由夾雜物尺寸決定,還與孔洞本身的生長機制有關。
圖6
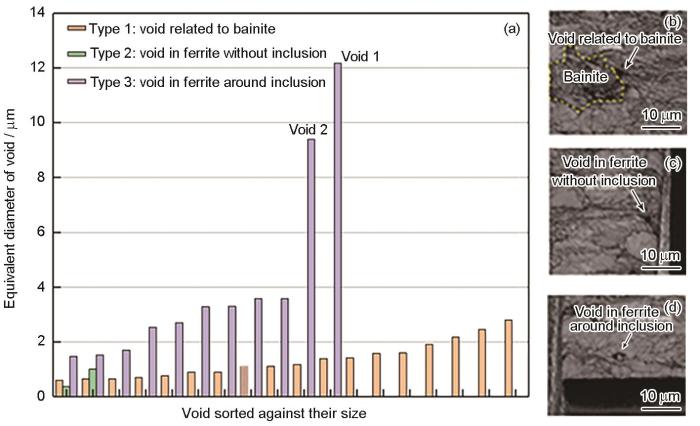
圖6 PFIB-SEM樣本(體積約98 μm × 98 μm × 80 μm)中孔洞的尺寸和類型,以及每種類型孔洞形貌的SEM像
Fig.6 Sizes and types of void in the PFIB-SEM sampled volume (~98 µm × 98 µm × 80 µm) (a) and SEM images of voids type 1 (b), type 2 (c), and type 3 (d)
Color online
圖7

圖7 孔洞尺寸與夾雜物尺寸的關系
Fig.7 Void size as a function of inclusion size
Color online
2.3 孔洞的生長機制
2.3.1 孔洞附近的塑性變形
由于位錯環(huán)或反平行位錯偶的形核和滑移是塑性誘發(fā)孔洞增長的重要機制,因此有必要研究鐵素體晶粒周圍的變形能力與孔洞尺寸差異的關系。bcc晶體具有多個密排面,主要滑移系有3種:{1
另外,由于夾雜物與基體彈性性質差異較大,夾雜物與基體界面局部塑性流動不均勻,存在應變梯度,因而需要產生幾何必需位錯(GND)來保持基體的連續(xù)性。為了研究孔洞周圍位錯密度與孔洞尺寸的關系,利用EBSD實驗測得的晶格轉動梯度求解了Nye位錯張量[35,36],計算方法在參考文獻[37~40]中有詳細介紹。孔洞與基體界面位置附近的GND密度取包含孔洞的所有EBSD切片的平均值,計算結果如圖8所示。從整體分布上可以看出,較小的孔洞周圍顯示出較高的GND密度,由此推測小孔洞周圍的高位錯密度造成了更強的硬化作用,進而抑制了孔洞的生長。這可以用來解釋圖7中觀察到的小孔洞生長率與宏觀應變的弱相關關系。
圖8

圖8 孔洞周圍的平均幾何必需位錯(GND)密度與夾雜物尺寸的關系
Fig.8 Average geometrically necessary dislocation (GND) density in the vicinity of voids as a function of associated inclusion size
2.3.2 孔洞的各向異性生長
由圖5可以看出,2個大的孔洞傾向于沿拉伸方向朝著夾雜物的一側生長,在微觀上孔洞的形狀呈各向異性。為了研究相鄰顯微組織對孔洞形貌的影響,計算了孔洞兩端的GND密度和Schmid因子,結果如圖9a1、a2和b1、b2所示。依據(jù)Hall-Petch關系,晶粒尺寸會通過位錯塞積產生的應力影響晶粒的變形能力,因此本工作引入了“加權Schmid因子(
式中,SFi 是第i個像素的Schmid因子,Di 是第i個像素所在晶粒的等效直徑。在此計算中,晶粒中每個像素的Schmid因子由相應晶粒的尺寸加權,因此較小晶粒中的Schmid因子被加權降低,而較大晶粒中的Schmid因子被加權提高。圖9a3~a6分別給出了孔洞的EBSD帶對比圖、Schmid因子分布圖、加權Schmid因子分布圖和GND密度分布圖。圖9a1為對圖9a3中孔洞兩側黃色虛線框區(qū)域統(tǒng)計平均GND密度,圖9a2為這2個區(qū)域的平均Schmid因子和平均加權Schmid因子。GND密度分布圖表明孔洞一側優(yōu)先生長,其累積滑移量比另一側大,Schmid因子分布圖也表明孔洞優(yōu)先生長一側的晶粒具有更高的變形能力。加權Schmid因子分布圖揭示了一些傳統(tǒng)Schmid因子圖無法顯示的有趣的特征,例如圖9a5中顯示的大孔洞右側的生長更傾向于向右下方的晶粒內延伸(晶粒4),這個晶粒擁有更高的加權Schmid因子,相比之下,孔洞右上方的晶粒尺寸很小,所以即便其具有更高的Schmid因子,但由于小晶粒尺寸Schmid因子被加權降低,所以晶粒不易塑性流動。
圖9

圖9 孔洞1和孔洞2的GND密度和Schmid因子,孔洞的EBSD帶對比圖、Schmid因子分布圖、加權Schmid因子分布圖和GND密度分布圖
Fig.9 GND densities (ρGND) (a1, b1) and Schmid factors (a2, b2) of the left and right parts around the voids in Figs.9a3 and b3; and EBSD band contrast maps (a3, b3), Schmid factor distributions (a4, b4), weighted Schmid factor distributions (a5, b5), and GND density distributions (a6, b6) of void 1 (a1-a6) and void 2 (b1-b6)
Color online
3 分析討論
3.1 孔洞的形核和生長
本工作所研究的鐵素體-貝氏體雙相鋼樣本中所有夾雜物顆粒都呈球狀且沒有發(fā)現(xiàn)夾雜物斷裂現(xiàn)象。樣品中大尺寸夾雜物主要是Al2O3夾雜,同時在其邊緣伴生有MnS形成復合夾雜物。其斷裂強度比鐵素體基體高3倍多,因此在這種材料中鐵素體/夾雜物的界面分離是變形過程孔洞形核的主要機制[8]。
從圖7可以看出,孔洞的尺寸與其相鄰的夾雜物尺寸密切相關,文獻[29]中也報道過類似的現(xiàn)象。從式(
式中,ρ為位錯密度,εp為塑性應變。可以看出,顆粒尺寸越小,其周圍位錯密度隨應變變化的速率越快,這與圖8結果以及文獻[42]的模擬結果一致。這些結果表明顆粒與基體界面的局部硬化率隨顆粒尺寸變化而變化,與大顆粒相比,小顆粒周圍的局部硬化會明顯高于基體。但是顆粒周圍的硬化速率并不是隨著顆粒尺寸的變化一直變化,當顆粒尺寸超過一定限度之后,界面與基體的應變將不再產生明顯差異,顆粒尺寸約束孔洞生長的效應也就不再明顯了。Goods和Brown[6]在Brown和Stobbs[41]理論的基礎上提出了臨界顆粒半徑(rc)的估算方法[6]:
式中,α是由材料本身決定的常數(shù)[43],µ是基體的剪切模量,σy是屈服應力,σ為工程應變?yōu)?i style=";padding: 0px;box-sizing: border-box">ε時所受的應力。如果顆粒尺寸小于rc,局部應變硬化率將會明顯超過基體并通過局部位錯的快速塞積制約孔洞生長,此時基于連續(xù)體力學的孔洞生長模型不再適用。對于較小尺寸的顆粒,如果局部硬化率高于基體,包裹隨后形核孔洞的林位錯可能會阻礙位錯的進一步滑移。在此條件下,外部載荷引起的局部塑性流動可以通過其他起始變形機制來實現(xiàn),比如臨近孔洞的加速膨脹或者硬化孔洞附近多滑移系的開動,這與文獻[44]中報道的孿晶尖端由于局部位錯硬化導致的孿晶不連續(xù)生長現(xiàn)象十分類似。
綜上所述,夾雜物的尺寸不僅影響孔洞形核的難易程度,也能夠通過局部位錯塞積影響孔洞的尺寸。這2種機制協(xié)同作用造成大夾雜物引起的孔洞較大、小夾雜物引起的孔洞較小的實驗現(xiàn)象。決定孔洞快速生長和慢速生長的夾雜物臨界尺寸可以利用Goods和Brown[6]提出的模型進行估算:將α = 0.3、b = 0.248 nm (α-Fe)代入
表1 不同鋼種依據(jù)式(6)的夾雜物臨界尺寸估算
Table 1
| Material | μ / GPa | σy / MPa |
|
rc / µm |
|---|---|---|---|---|
| Low-carbon steel | 80 | 295 | 200 | 2.06 |
| Ferrite in ferrite-bainite dual-phase steel[45] | 72 | 370 | 106 | 2.51 |
| Bainite in ferrite-bainite dual-phase steel[45] | 76 | 830 | 258 | 0.51 |
| Ferrite in 600 MPa ferrite-martensite dual-phase steel[46] | 78 | 313 | 160 | 2.30 |
| Martensite in 600 MPa ferrite-martensite dual-phase steel[46] | 79 | 1014 | 167 | 0.32 |
| Ferrite in 1000 MPa ferrite-martensite dual-phase steel[46] | 78 | 443 | 141 | 1.85 |
| Martensite in 1000 MPa ferrite-martensite dual-phase steel[46] | 79 | 813 | 280 | 0.52 |
| Ferrite in ferrite-martensite dual-phase steel[47] | 79 | 260 | 159 | 2.86 |
| Martensite in ferrite-martensite dual-phase steel[47] | 79 | 1000 | 460 | 0.26 |
| Ferrite in ferrite-martensite dual-phase steel[48] | 77 | 430 | 117 | 2.24 |
| Martensite in ferrite-martensite dual-phase steel[48] | 77 | 1450 | 431 | 0.18 |
Table 2
| Material | Matrix | Inclusion type | Critical size of inclusion / µm | Ref. |
|---|---|---|---|---|
| Steel | Ferrite | Silicate, TiN | 2-4 | [49] |
| A508 steel | Bainite | MnS | 17 × 10 × 3 | [50] |
| SAE52100 | Martensite | Ca-Al-O, Ti(N, C) | 21 | [51] |
| 600 MPa high-strength steel | Martensite | Inclusion | 2 | [52] |
| Ferrite-martensite dual-phase steel | Ferrite + martensite | Inclusion | Correlated with martensite phase size | [48] |
| High-strength steel | Martensite | Al2O3 | 16 | [53] |
| High-strength steel | Martensite | TiN | 11 | [53] |
| Bearing steel | Martensite | Mg-Al-O | 8.5 | [54] |
| Bearing steel | Martensite | Calcium aluminate | 13.5 | [54] |
| Pipeline steel | Ferrite + pearlite | MnS | 2.52-2.6 | [55] |
| SLM IN718 | Ni suppralloy | Void | 20 | [56] |
由表1可大致確定鐵素體中夾雜物周圍孔洞形核的臨界尺寸在1.85~2.86 µm之間,與本工作估算值吻合較好;且從表1可以看出,受貝氏體和馬氏體較高的彈性模量和加工硬化率影響,其內彈性應力在加載過程中累積速率高于基體,因此其內部夾雜物的臨界尺寸相對較低,貝氏體臨界尺寸約為0.51 µm,馬氏體臨界尺寸在0.18~0.52 µm之間。本工作臨界尺寸與表2[48~56]中個別文獻報道吻合,但大部分文獻報道的臨界尺寸整體較高,這可能與具體分析方法的空間分辨率有關。除此之外,由于靠近孔洞位置的EBSD解析率降低且材料整體變形嚴重,圖8中呈現(xiàn)的位錯分析標準誤差較大,因此夾雜物尺寸與局部位錯密度的關系模型難以建立。需要使用變形程度較低的材料以及一些先進的衍射花樣標定方法來進行改進,如具有更好魯棒性和更高分辨率的字典算法[57,58]。
3.2 孔洞的擇優(yōu)生長及晶粒尺寸的影響
在大孔洞的延伸過程中可能存在如圖9所示的擇優(yōu)生長現(xiàn)象,即孔洞并非以夾雜物為中心向外均勻擴展,這種生長模式在文獻[59,60]中也有報道。仔細研究孔洞周圍顯微組織可以發(fā)現(xiàn),孔洞的擇優(yōu)生長不是隨機的,而是由周圍晶粒的微織構控制的,正如圖9a4、a6和圖9b4、b6 所示孔洞擇優(yōu)生長一側的Schmid因子和GND密度都要高出另外一側。圖9a6所示孔洞中右側晶粒1~3都表現(xiàn)出較高的Schmid因子,但由于它們的晶粒尺寸較小,因此不利于孔洞生長。晶粒4具有更大的尺寸和同樣高的Schmid因子,因此孔洞更傾向于向晶粒4一側生長。從圖9a5中同樣可以看出,大孔洞與右邊的小孔洞進行連接合并十分困難,這是因為連接孔洞的晶粒1、2和3由于較低的加權Schmid因子無法提供足夠的塑性流動來激發(fā)合并機制(局部縮頸或局部剪切[5])。由此可以認為,在本工作鐵素體-貝氏體雙相鋼內只包含小顆粒的情況下,由于孔洞本身生長會受到制約,通過孔洞生長導致塑性斷裂的可能性較低,這種情況下塑性斷裂主要取決于孔洞的間距和分離孔洞的基體的變形能力。對于孔洞間織構上較軟的基體(高SFi*),塑性流變可以較快縮減孔隙間距,導致孔洞在相對較低的應變下發(fā)生連接合并,形成微裂縫并最終導致斷裂。
4 結論
(1) 使用多模態(tài)關聯(lián)的表征分析方法研究了鐵素體-貝氏體雙相鋼韌性斷裂過程中孔洞的生長行為及孔洞周圍局部微觀結構對孔洞生長的影響。受限于XCT實驗的空間分辨率,實驗過程只觀察到了鐵素體中2 µm以上夾雜物導致孔洞形核的現(xiàn)象,但是通過關聯(lián)性3D-EBSD表征,發(fā)現(xiàn)貝氏體中尺寸小于2 µm的夾雜物也引發(fā)了孔洞形核。與貝氏體相比,鐵素體相中的夾雜物會導致更大的孔洞,這主要與鐵素體相的變形抗性較弱或者鐵素體中夾雜物誘發(fā)孔洞形核所需的應變整體較低有關。
(2) 孔洞的生長受夾雜物尺寸效應影響顯著,較小的夾雜物會引起局部高位錯密度包殼阻礙位錯滑移,從而限制孔洞的生長。通過解析理論模型,根據(jù)所研究材料的性質,計算出在鐵素體相中夾雜物形核的臨界尺寸在1.85~2.86 µm之間,低于這個臨界尺寸的夾雜物,孔洞周圍由于受到強變形梯度塑性的影響生長緩慢,高于這個臨界尺寸的夾雜物則可導致孔洞的快速生長從而顯著降低塑性與斷裂韌性。
(3) 單向拉伸變形過程中,孔洞主要沿著加載方向生長,但孔洞周圍晶粒的微觀織構會改變其生長方向,表現(xiàn)出各向異性。孔洞的復雜形狀可以用Schmid因子和晶粒尺寸相結合的加權Schmid因子進行預測。孔洞連接合并的難易程度會受到分隔孔洞之間基體材料的晶粒尺寸和織構的影響。
(4) 3D-EBSD晶粒尺寸表征結果顯示,真實三維晶粒尺寸計算結果是二維表面計算結果的3倍左右,因此需謹慎對待二維表面晶粒度的測量結果。
來源--金屬學報





 滬公網(wǎng)安備31011202020290號
滬公網(wǎng)安備31011202020290號
